ノイズスケジューラの動作確認

Section 03: Basics of Diffusion Model の Lecture 09: Denoising Diffusion Probabilistic Model (1) にて、ノイズ除去拡散確率モデル (denoising probabilistic diffusion model; DDPM) [Ho+ NeurIPS'20] について説明しました。

拡散過程において付与されるノイズは ノイズスケジューラ によって決定します。以下、ノイズスケジューラの簡易的な実装方法について紹介します。

拡散過程 - forward diffusion process

拡散過程はステップ \(0\) から \(T\) まで入力画像に徐々にノイズを加えていくものです。この過程は関数 \(q\) として、以下のように定義されます:

\[ q(\boldsymbol{x}_t | \boldsymbol{x}_0) = \mathcal{N}(\boldsymbol{x}_t; \sqrt{\bar{\alpha}}_t\boldsymbol{x}_0, (1 - \bar{\alpha}_t)\boldsymbol{I}). \]

ここで \(x_0\) は初期ステップでの画像 (元画像) であり、\(x_t\) はステップ \(t\) におけるノイズ画像です。\(\bar{\alpha}_t\) は付与するノイズを決定するノイズスケジューラです。

ノイズスケジューラの定義

ノイズスケジューラ \(\bar{\alpha}\) は次のように定義されます:

\[ \bar{\alpha}_t = \prod_{s=1}^t \alpha_s. \]

ここで \(\alpha_t\) は次のように定義されます:

\[ \alpha_t = 1 - \beta_t. \]

スケジューラの値が小さいほどより多くのノイズが追加されます。DDPM [Ho+ NeurIPS'20] では、\(\alpha_t\) を \(1 - \beta_t\) として定義し、\(\bar{\alpha}\) をステップ \(0\) から \(t\) までの \(\alpha\) の累積積として使用しています。

以上より、今度は \(\beta_t\) がノイズスケジューラとなります。DDPM [Ho+ NeurIPS'20] では \(10^{-4}\) から \(0.02\) の間の値を示す線形スケジューラを使用しています。これらの値はステップ \(t-1\) に対する \(t\) で追加されるノイズの量を示すパーセンテージのようなものを表していると考えられます。

ノイズスケジューラの実装

まず \(\bar{\alpha}\) は次のように実装できます:

def alpha_bar(t: int, T: int) -> float:
    alpha_values = [alpha(s, T) for s in range(t)]
    ret = 1
    for alpha_value in alpha_values:
        ret *= alpha_value
    return ret

次に \(\alpha_t\) は次のように実装できます:

def alpha(t: int, T: int) -> float:
    return 1 - beta(t, T)

最後に \(\beta_t\) は次のような線形スケジューラとして実装できます:

def beta(t: int, T: int, upper: float = 0.02, lower: float = 10 ** -4) -> float:
    if t == 0:
        return lower
    return (upper - lower) / T * t + lower

ノイズスケジューラの動作可視化

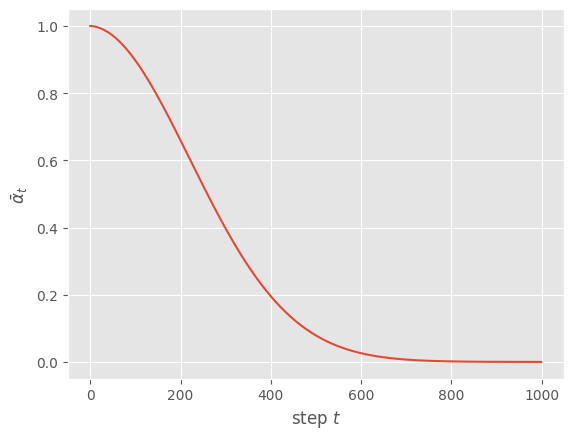
上記で実装した式を使用して、ノイズスケジューラの動作を可視化してみます。\(T = 1000\) として設定し、\(\bar{\alpha}_t\) の値を計算します。

T = 1000
ts = list(range(T)) # 0 ~ T までの値が入ったリストを作成

alpha_bar_values = [alpha_bar(t, T) for t in ts]

上記で得た \bar{\alpha}_t を元にグラフにプロットしてみます。

import matplotlib.pyplot as plt
plt.style.use("ggplot")

fig, ax = plt.subplots()
ax.set_xlabel("step $t$")
ax.set_ylabel("$\\bar{\\alpha}_t$")
ax.plot(ts, alpha_bar_values)

[<matplotlib.lines.Line2D at 0x7a59ae855450>]